The Algebraic Integral Calculator, A Very Unusual Calculation Device, Created By David@TechForText.com

The Algebraic Integral Calculator: Simple Three Step Instructions

1) To enter or delete numbers, left click with the mouse on the relevant white input box.

2) Delete the numbers in the following three white input boxes, and enter your own numbers.

3) For results, left click with the mouse on the calculation button, or yellow background.

The exponent: n =

Area under the curve: M =

A =

The Algebraic Integral Calculator was created in Microsoft Excel, and it was converted to JavaScript. The formulas used to create this software are shown in the Excel format for illustration purposes.

In the white input boxes, n, M, and A, were defined with the name mechanism in Microsoft Excel. As a result, the letters are recognized by the computer, in terms of the numbers entered in the input boxes.

This provides the functionality needed for creating spreadsheet formulas using letters and/or words.

B is the Calculated Result

An integral is usually solved for the area under a curve, but that is NOT what we are doing here. We are calculating the value of B

B =

The Numbers in red type, are calculated results, or numbers transmitted from one cell to another by this software.

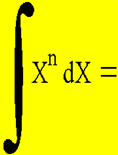A fraction of a second after calculating the value for B, this software calculates the area under the curve, (from B to A) to check the calculated results.

M =

This software compares the calculated area, and the area entered by the user, to determine the accuracy of calculations.

A =

The spreadsheet formulas from above are presented below, (with their error messages).

For B =IF((ABS(C50)>L45),"NO CALCULATED RESULT FOR THE NUMBERS YOU ENTERED",ROUND(B, M42))

The above displays the value of B, but B is calculated elsewhere, with this formula: =(M*(n+1)+A^(n+1))^(1/(n+1))

For A =IF((ABS(C51)>L46), "NO CALCULATED RESULT", ROUND(A, M42))

For M =IF( (ABS(C51)>L46), "NO CALCULATED RESULT", ROUND(M, M42))

Calculations for the XY-Coordinates for the Area Under the Curve

The calculations for the XY-coordinates of the area under the curve from

point (A, Aⁿ) to point (B, Bⁿ) are carried out by the software, with the

numbers that were entered by the user, which are listed below:

Number entered by user A =

This is a calculated result B =

Number entered by user n =

The curve is produced by this equation: Y

= X

X-Y-Coordinates when X=A is calculated below

X_a = A

Y_a = f(A) = Aⁿ

X-Y-Coordinates when X=B is calculated below

X_b = B

Y_b = f(B) = Bⁿ

Note, the area under the curve is calculated in the last section

Mechanisms for: Rounding down, Error-Checking, Measuring Error and Accuracy

All of the numbers ABOVE are automatically rounded to

decimal places.

You can increase or decrease the number of decimal places, by deleting the

blue number, above, and entering the number of decimal places you prefer

When numbers have

decimal places, or less, they are not rounded.

Note, the error-checking device, presented below, has its own rounding mechanism.

In general, computer calculations are usually accurate to at least 10 or 15 decimal places. However, with certain number combinations, or when many digits are

involved, there may be a lower level of accuracy. The Algebraic Integral Calculator has a user controllable mechanism, below, to prevent the display of calculation

results that deviate from accuracy by a specific percentage.

Calculated result with an error greater than

will NOT be displayed.

If you want a greater or lesser level of acceptable error, delete the blue number,

above, and enter the number you prefer. The smaller the number, the greater the

accuracy. The number you enter can be a decimal, such as 0.001 % or it can

even be zero.

All of the numbers for the Error-Checking are rounded to

decimal places.

This is done, to prevent rounding errors, in the error-checking mechanism.

You can increase or decrease the number of decimal places, by deleting the

blue number, above, and entering the number of decimal places you prefer.

If you enter a number that is too large, you will see rounding errors.

Note, this rounding mechanism does not affect the number of zeros displayed.

The Error-Checking and Measuring Mechanism of the Algebraic Integral Calculator

This device calculates the error in percent, which is presented below in red type.

Spreadsheet formula (Percentage Format) for above is: =ROUND( (CalculatedM -M)/M, M55 )

The above error-checking and measuring mechanism functions by comparing the value the user entered for the area under the curve, and the calculated value for the area

under the curve. In the formulas, M is the value the user entered for the area, and the calculated value for the area is represented by CalculatedM. This can be seen above

in the spreadsheet formula, and in the conventional formulas presented below.

Keep in mind that the values the user entered were used to calculate B. Then the calculated area was obtained using the values for B, A, and n.

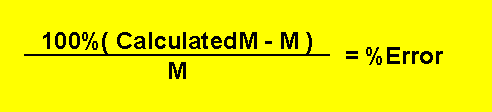The above formula, and error-checking device measures the degree of error. Low numbers, or zero means little or no error.

The following device and related formula are similar to the above, except it calculates the degree of accuracy, instead of the degree of error. The device and the formula,

calculate accuracy by dividing the calculated area, (CalculatedM) by the area the user entered (M). This ratio is multiplied by100% This can be seen in the following formula.

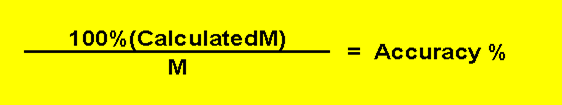With the above formula, and the device presented below, the higher the number, the greater the accuracy. A perfectly accurate calculation is 100% accurate.

This device calculates the percent of accuracy

Spreadsheet formula (in Percentage Format) for above is: =(CalculatedM-M)/M

The Area Under the Curve is

In this section, the calculated results, and numbers obtained from other sections of the calculator are NOT rounded down to a predetermined number of decimal places.

This is because the numbers are used for additional calculations, on several sections of the Calculator.

The spreadsheet formula for the following is =(M*(n+1)+A^(n+1))^(1/(n+1))

The value of B was defined below, with the Microsoft Excel name mechanism

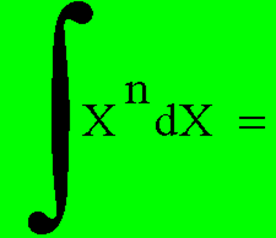Below, is the calculated value of the area under the curve, based on the calculated value for B. This is the calculated value of M, and it is

defined as: CalculatedM with the Excel name mechanism.

The spreadsheet formula for the above is: =(( B^(n+1) - A^(n+1) )/(n+1))

This formula calculates the area under the curve.

A =