
Strategies for Studying, Learning, and Researching
By David Alderoty © 2014
Chapter 6)Types of
Reasoning: Visual, Verbal, Mathematical, and Deductive & Inductive Reasoning
4,379 Words
If you want to go to the previous chapter,
left click on the link below
www.TechForText.com/SL/Chapter-5
To contact the author left click for a
website communication form, or use:
If you want to go to the table of contents
of this chapter left click on these words
To Access Additional Information with Hyperlinks
After I complete a writing task, I select a number of websites from other authors, to provide additional information, alternative points of view, and to support the material I wrote. These websites contain articles, videos, and other useful material. The websites can be accessed by clicking on the hyperlinks, which are the blue underlined words, presented at the end of some of the sections, subsections, and paragraphs. If a link fails, use the blue underlined words as a search phrase, with www.Google.com or www.Bing.com
Reasoning: Introductory Concepts
A good understanding of logic and reasoning is helpful for mastering courses that involve writing, mathematics, science, critical thinking, and philosophy. In this chapter, I present some conventional and unconventional concepts on various types of reasoning. This includes visual, verbal, and mathematical reasoning, as well as a detailed discussion of deductive and inductive reasoning.
Reasoning for Comprehension, and Reasoning for Solving Problems, and Creating Entities
Based on the way am using the terminology, reasoning involves two concepts, which I am calling reasoning input and reasoning output.
Reasoning input involves comprehending information, and recognizing any logical relationships or fallacies that it may contain. This process takes place when we truly understand the material we are reading, listening to, and/or viewing. This deep level of understanding facilitates learning and memory.
Reasoning output involves creating and/or organizing entities, based on a set of rules or the requirements to obtain a goal or solve a problem. The entities can be physical structures, information, logical configurations, words, mathematical concepts, visual elements, or anything else. The set of rules can involve any of the following:
Playing a game, especially if it involves logic
Creative thinking
Mathematical or logical concepts
Writing an essay, a term paper, a business report, poetry, a novel, or a computer program
Any type of mathematics, logic, or reasoning, including deductive or inductive reasoning
I am dividing thinking and problem solving into three categories, which are visual reasoning, verbal reasoning, and mathematical reasoning. There is some overlap between the three categories. For example, certain types of mathematical reasoning also involve visual and/or verbal reasoning.
If we apply the concept presented in the previous subsection to the three categories there is an input and output version for visual reasoning, verbal reasoning, and mathematical reasoning. This is explained in detail under the following three headings.
Visual Reasoning, and Related Concepts
Visual Reasoning for Comprehension, & Problem Solving
Based on the way I am using the terminology, visual reasoning involves two concepts, which I am calling visual reasoning input, and visual reasoning output.
Visual reasoning input involves comprehending visual relationships, shapes, and logical configurations presented in a visual format.
Visual reasoning output involves arranging, shaping, or building objects, based on a set of rules, or on a specific objective. This includes modifying structures, and problem solving that is based on visible entities.
People that have been blind since birth can carry out visual reasoning input and output, with the sense of touch. Individuals that became blind after they were born might have the ability to create visual images in their mind, based on the sense of touch. This involves interpreting visual relationships, and changes in visual configurations, with the sense of touch. Sighted people might also use the sense of touch under certain conditions, to assist them with visual reasoning.
The following are examples of visual reasoning, but some of the items in this list, might also require mathematical or verbal reasoning:
EXAMPLES OF VISUAL REASONING INPUT
Comprehending the logical concepts and relationships in any type of diagram or blueprint
Inspecting and comprehending any visual entity, such as a work of art, a map, or any three dimensional structure
Examining and comprehending the components and related dynamics of a mechanical or electrical device
Recognizing any entity, with the aid of vision
EXAMPLES OF VISUAL REASONING OUTPUT
Arranging toy blocks into a configuration that resembles a house
Creating a blueprint on paper, to build a real house
Playing a game of checkers, chess, or tic-tac-toe
Creating an organizational chart, with the lines of communication and authority
Creating a visual depiction of a flow pattern of electricity, data, or fluid, from one component to another
Creating pottery with clay
Creating a sculpture with marble
Any construction or engineering project (This includes building and/or designing an entity, such as an electronic circuit, an automobile, a jet plane, a house, or skyscraper.)
Verbal Reasoning and Related Concepts
Verbal Reasoning for Comprehension, & Problem Solving
Based on the way I am using the terminology, verbal reasoning involves two concepts, which I am calling verbal reasoning input, and verbal reasoning output.
Verbal reasoning input involves comprehending written and/or spoken language, and identifying logical relationships, and fallacies contained in a statement. This includes evaluating arguments, based on deductive reasoning.
Verbal reasoning output involves arranging words into arguments, phrases, sentences, or paragraphs, based on a set of rules, and/or based on one or more goals. In general, it also includes using written or spoken language, to convey information, or to describe a concept or entity. This includes writing essays, poetry, or term papers. This also includes creating arguments with deductive reasoning, and proving or evaluating logical relationships with premises.
Verbal Reasoning, and Logical Statements
Verbal reasoning can involve various types of logical statements, which are used in written and spoken language. Many of these statements are quite simple, and most six-year-olds will have no difficulty understanding them. However, the simple statements can be connected together in very complex ways. These statements can be converted to various types of symbolic formats, and used in electronics and computer technology. See the following examples:
IF THEN STATEMENTS: The general example is IF A, then B.
A specific example is if it rains, the game is canceled.
AND STATEMENTS: The general example is A and B.
A specific example is Mike and Susan will help you tomorrow.
OR STATEMENTS: The general example is A or B.
A specific example is Mike or Susan will help you tomorrow.
Additional examples with premises are presented below:
IF THEN STATEMENT: If John is in Washington, then his cell phone is in Washington. PREMISE: John always takes his cell phone wherever he goes.
IF THEN STATEMENT: If Susan is in Connecticut, so are her legs. PREMISE: Susan’s legs are attached to her body
IF THEN STATEMENT: If the display light is on, so is the radio. PREMISE: The display light is part of the radio, and is connected to the on off switch.
IF THEN STATEMENT and OR STATEMENT: If the display light is off, the computer is not on, or the display light burnt out. PREMISE: The display light is designed to turn on, when the computer is on, but if it is burnt out, it cannot turn on, even if the computer is on.
Verbal Reasoning: Two Categories of Logical Statements
Logical statements can be placed into two general categories. The first category involves logical statements that are based on factual principles of nature, circumstances, or wording. For example, if the mayor is in Washington, then his arms and legs are also in Washington. I am calling this category, statements based on natural rules. The truth or validity of statements in this category, are not determined by rules created by human beings.
The second category involves logical statements that are based on rules created by human beings. This essentially involves manufactured logical relationships, which do not exist in nature. This concept is important because it is used in law, electronics, computer science, and many other fields. This is illustrated with the four examples presented below. Note, the manufactured logical relationships are highlighted in yellow.
Example 1, relates to law) If you are in New York City, and your automobile speedometer indicates 95 miles an hour, you are breaking the law, and guilty of speeding.
Example 2, involves electronics) A LCD light is connected to the on off switch of an electronic device. This represents a simple logical statement, which is, if the LCD light is glowing, the device is turned on.
Examples 3 and 4 involve computer technology, and they are based on simple logical statements, connected together into complex configurations. These examples are illustrated in more detail with online software, presented on the websites indicated in the examples. I created this software in 2012, for my undergraduate studies, initially with Microsoft Excel. The Excel version was electronically converted to JavaScript code, to create the online version. The examples are illustrated with the logical statements in the Excel format.
Example 3) www.TechForText.com/Using-One-Symbol-to-Represent-a-Set-in-Programming The software on this website demonstrates that one symbol can be used to represent a set of symbols, such as the following:
A={Set of words you entered in input Box-One}
B={Set of words you entered in input Box-Two}
C={Set of words you entered in input Box-Three}
I created this software with a number of manufactured logical statements, involving if then. I translated the statements to a symbolic format that a computer running Microsoft Excel can comprehend. See the following:
=IF(B30="",B31,B30), =IF(B39="",B40,B39), =IF(B48="",B49,B48), =IF(B57="",B58,B57 ), =IF(B66="",B67,B66), =IF(B75="",B76,B75 ), =IF(B84="",B85,B84), =IF(B93="",B94,B93), =IF(B102="",B103,B102), =IF(B111="",B112,B111)
Example 4) www.TechForText.com/Computing-Devices-Relativity-of-Meaning This software demonstrates the relativity of the meaning of symbols in computing devices. It has three mechanisms that interpret the meaning of red, blue, and green, in three different ways.
I created this software with a number of manufactured logical statements, involving if then. I translated the statements to a symbolic format that a computer running Microsoft Excel can comprehend. See the following:
=IF(I4="","",I4), =IF(D5="red", C20, "")&IF(D5="Blue", C21, "")&IF(D5="Green", C22, ""), =IF(J5="Red",I20,""), =IF(J5="Blue",I21,""), =IF(J5="Green",I22,""),
=IF(O4="red",O20, "")&IF(O4="Blue", O21, "") &IF(O4="Green",O22,"")
Mathematical Reasoning, and Related Concepts
Mathematical Reasoning for Comprehension, And Problem Solving
Based on the way I am using the terminology, mathematical reasoning involves two concepts, which I am calling mathematical reasoning input, and mathematical reasoning output.
Mathematical reasoning input involves comprehending mathematical logic, formulas, concepts, geometric relationships, graphic representations, and algebraic expressions. This includes reading and understanding a document with mathematics.
Mathematical reasoning output involves creating mathematical concepts and expressions, or solving problems that involve mathematics. This includes interpreting and writing various types of data in a mathematical format, such as verbal statements, and visual or geometric information. It also includes the process of proving any geometric, trigonometric, and algebraic relationship, with deductive reasoning, or with experimentation.
Reading and Learning Mathematics
Mathematical reasoning input, includes examining, or reading mathematical concepts and expressions. Unlike conventional reading, this process must be carried out at a relatively slow rate. For example, reading a page from a social science textbook might require five minutes. If you are studying unfamiliar social science concepts, it might require 15 minutes per page. However, if you are reading a page with mathematical principles, or instructions for solving math problems, it might require anywhere from 20 to 40 minutes for each page. If you are unfamiliar with the mathematical concepts or formulas, it might require more than one hour for each page. This usually requires reading material several times, and solving a series of mathematical problems, to comprehend the unfamiliar material.
Many people do not understand the above, and they may attempt to read mathematical material in a way they would read a book on sociology. People that do this usually think they are terrible in math. However, the problem is they are using the wrong reading and studying strategies, for subjects that involve mathematics. This can make it difficult, or impossible, to successfully master courses involving mathematics.
The concepts presented above are well known by anyone that is reasonably successful with mathematics. For additional information, see the following three websites: 1) How to Read Mathematics 2) HOW TO LEARN FROM A MATH BOOK 3) Tips for Reading Your Mathematics Textbook
Mathematical Reasoning in General
Mathematical reasoning often involves verbal and/or visual reasoning, with numbers, letters that represent numbers, graphs, or diagrams. Verbal reasoning is most apparent with mathematical problems presented in written language. This requires a translation to a mathematical format, to solve the problem. Mathematical proofs that involve deductive reasoning with axioms, postulates, and theorems, also involve verbal reasoning. The use of visual reasoning is most obvious with geometric calculations and proofs.
Deductive & Inductive Reasoning, with Related Concepts
Introductory Note on Variations in the Descriptions of Deductive and Inductive Reasoning
Deductive and inductive reasoning are used in mathematics, science, and engineering. The websites that I encountered, with a philosophical focus, described deductive and inductive reasoning, with an emphasis that was somewhat different from the conventional scientific perspective. They emphasize the precision and accuracy of deductive reasoning, and describe inductive reasoning as less precise. This is only true, if all the premises are correct in a deductive argument.
Inductive reasoning is used in the sciences, and it can be extremely precise, especially if conclusions are evaluated experimentally. This is obvious, from the extremely precise and powerful technologies that were developed from the sciences.
For the philosophical point of view, see the following three websites: 1) “Internet Encyclopedia of Philosophy (IEP)”, 2) “Arguments and Inference” The following website, points out some of the deficiencies with the conventional definitions and descriptions of deductive and inductive reasoning. 3) Philosophy 103: Introduction to Logic
The websites that did not have a philosophical focus described deductive and inductive reasoning, in a manner that is consistent with the conventional descriptions presented in science and mathematics. My descriptions are based on the conventional descriptions, because they are more relevant for the material in this e-book.
See the following four websites for typical delineations of inductive and deductive reasoning: 1) Deductive Reasoning Versus Inductive Reasoning 2) Deduction and Induction 3) Inductive vs. Deductive Reasoning 4) Induction Vs. Deduction Economics My description of deductive and inductive reasoning is presented under the following subheadings.
Deductive reasoning usually starts with a general concept, which is narrowed down to a specific case. For a simplified example, let us assume that insects are six legged creatures, with a three-segment body structure, with wings. This is a general statement, which in this case happens to be a definition, (which is somewhat simplified). Let us assume you see a butterfly, and you notice that it is a six legged creature, with a three-segment body structure, with wings, which is an example of a specific case. Your conclusion is the butterfly is an insect, which is true by definition.
The above is a simplified example of deductive reasoning. Below there is a more complex explanation.
Deductive reasoning involves a proposition, which is a general statement that may be true or false. This is followed by one or more premises that lead to a conclusion. The premises are statements that are known to be true, or are assumed to be true. Premises can be axioms, postulates, theorems, scientifically verified theories, and definitions. The *conclusion indicates whether the proposition is true or false. Deductive reasoning is sometimes described as top-down reasoning. This is because it starts with a proposition, followed by one or more premises that logically lead to a conclusion.
*Note, sometimes deductive reasoning can involve statements that are conditionally true, or other types of conclusions, such as butterflies are insects.
Sometimes the premises in deductive reasoning are not stated, but they are implied by the wording and logical structure of the argument. When the premises are stated, the reasoning is likely to be very precise. Deductive reasoning, with stated premises, is especially useful for proving mathematical and geometric concepts.
Deductive Reasoning, with Verbal and/or Visual Reasoning
Most deductive reasoning is based on verbal reasoning. However, in some cases there may be both verbal and visual reasoning involved. For example, geometric proofs usually involve visual reasoning with diagrams, and verbal reasoning with postulates and theorems. In many cases, it is possible to convert deductive reasoning to a visual format, using various types of diagrams. When this is done, visual reasoning is involved. See the following example.
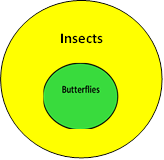
The above is called a Venn Diagram, and it indicates the conclusion, which in this case is butterflies are insects. This can also be stated as insects represent a set of six legged creatures, with a three-segment body structure, with wings. This set is represented by the yellow circle. Butterflies are a subset of the above, because they are six legged creatures, with a three-segment body structure, with wings. A subset is a smaller set, contained within a larger set. The small green circle is the set of butterflies, and it is contained within the larger yellow circle, which represents the set of all insects.
Diagrams do not always clarify or simplify deductive reasoning, and in some cases, it may make it more confusing. However, if you want more information see the following six websites: 1) Venn Diagram Solution, 2) Venn Diagrams and Logic, 3) DEDUCTIVE LOGIC AND VENN DIAGRAMS, 4) With Venn Diagrams Optional, 5) Solving Word Problems with Venn Diagrams, part 1, 6) Solving Word Problems with Venn Diagrams, part 2
Writing, with an Informal Deductive Reasoning Structure
An *informal type of deductive reasoning is frequently used in writing. For example, a college essay often starts with a thesis, which is analogous to a proposition in deductive reasoning. The thesis is supported or proved in the body of the text, with premises. This leads to a conclusion, which can be more or less similar to a conclusion from deductive reasoning. The same general idea applies to an academic thesis, and even some business reports.
*However, arguments in written language are often based on evidence, which leads to a conclusion, which does not fit the requirements of formal logic. This is, because evidence usually does not consist of indisputable premises. Evidence suggests or indicates the possibility or likelihood that an argument and related conclusion might be correct.
In addition, the premises in formal logic are logically related to the conclusion, and if one of the premises turns out to be false, the entire argument is invalid. This is not the case with evidence. For an example, let us assume a murder suspect was arrested because his blood, DNA, hair, and fingerprints, was found on the crime scene, and video surveillance shows him committing the murder. If it turned out that the blood, hair, and fingerprints, was not from the suspect, the video surveillance, and DNA would be adequate evidence for conviction.
Inductive reasoning is sometimes described as the opposite of deductive reasoning, or as bottom-up thinking. This is because it starts with observation of specific cases, to create a general concept, or a hypothesis, which is the conclusion. That is, inductive reasoning, usually involves examining a relatively small number of entities in a specific category, and devising a general principle that applies to all entities in the category. The following example will clarify this concept.
Let us assume, you examine 10 species of spiders, and they all have eight legs. Then your conclusion is a general statement, which is all spiders have eight legs. How accurate is this conclusion? Conclusions derived with inductive reasoning are not considered 100% accurate, because they are usually based on a limited number of samples. Using the example with spiders, there is a possibility that if you examine more spiders, you may find that there are spiders with six legs.
Conclusions From Deductive Reasoning Can Sometimes Be Converted To Definitions That are Indisputable
Sometimes conclusions from deductive reasoning can be changed into indisputable definitions. To clarify this idea, I will return to the example presented in the previous subsection, which involve the conclusion (or hypothesis) that all spiders have eight legs. This hypothesis can be converted to an indisputable definition by defining the word spider (or any other suitable term) as a small creature with eight legs. Thus, if someone found a new creature that resembled a spider, with six legs it would not be a spider by definition, and it would not contradict your conclusion.
The above essentially involves defining the observed or experimental sample with precise terminology. The following example will provide further clarification of this idea, in terms of social science.
Let us assume that a scientifically designed survey is carried out on an ethnic group X, and the results indicate 97% of the sample was exceptionally self-disciplined. Instead of saying that people in ethnic group X are extraordinarily self-disciplined, you can create a definition for highly self disciplined people in ethnic group X, such as disciplined-Xs. Then you can state that based on your survey 97% of the ethnic group X are disciplined-Xs.
With the above technique, further study can be carried out based on the category defined by the definition. For example, additional studies can be carried out on the disciplined-Xs, such as to determine how they became highly self-disciplined, and to determine how this affects their achievements in school and employment.
Checking the Validity of Inductive Reasoning
The hypotheses derived with deductive reasoning, usually cannot be converted to indisputable definitions. In such a case, the hypothesis must be evaluated experimentally. With published work, this usually involves a number of experiments, carried out by different researchers, over a period of months or years to assess the validity of a hypothesis. With unpublished work, a hypothesis can be evaluated with a few experiments, which can be informal in structure.
Checking Inductive Reasoning in Everyday Life
Most people derive assumptions or hypotheses, about other individuals, products, service providers, and vendors. People also derive assumptions about their own capabilities as well as the abilities of others. These assumptions are conclusions derived with an informal version of inductive reasoning. I am calling conclusions in this category, personal assumptions, or personal hypotheses. The *relative degree of validity of these assumptions should be tested with informal experimentation, when feasible. Sometimes-ongoing experience with a person, product or other entity, can determine the relative degree of validity of your personal assumptions.
*I used the words relative degree of validity, because many of the conclusions we derive in everyday life are partly true and partly false, or conditionally true. For example, we may find that a service provider is very angry and unfriendly at the end of the day, when he is overwhelmed with too many clients. At other times, he may be quite friendly. Thus, the assumption that he is a hostile person would be only partly correct, or conditionally true.
It is important, and sometimes difficult to recognize personal hypotheses that are incorrect, and to abandon them. However, this process is likely to be much easier, if you assume that your personal hypotheses might be erroneous, partly correct, conditionally true, or perfectly correct. In addition, you should never stake your reputation on any unproven hypotheses. If you do, it may be embarrassing, and a risk to your reputation, if the hypothesis is determined to be incorrect.
Can Inductive Reasoning Be as Precise as Deductive Reasoning?
There are certain types of inductive reasoning that can be as precise as deductive reasoning. In the previous subsection, one of these examples was presented, which involved inductive conclusions that can be converted to definitions. There are other variations of inductive reasoning that have a similar level of precision, presented with the following four examples.
____EXAMPLE 1____
When a problem involves a precise set of entities forming a pattern, or sequence of numbers, it is usually possible to devise a related hypothesis, based on observation that is certain. For example, what is the missing number in the following sequence: 0, 4, 8, 12, 16, ? The solution is presented below:
The hypothesis I derive from observation is any number in the sequence is represented by the formula N+4=Next number in sequence. Thus, when N=16, thus, 16+4=20 Conclusion: the missing number is 20 That is 0, 4, 8, 12, 16, 20
____EXAMPLE 2____
The following is an example of a pattern comprised of *: (),(***),(******),(*********),(?) Find the pattern that belongs in the parentheses with the question mark.
The hypothesis derived by observation is the number of * in any section of the sequence, can be determined with the following formula: X*+3*=Next number of * in a following pattern. Thus, X*=(*********)=9* Then 9*+3*=12* Thus, conclusion is (************)
____EXAMPLE 3____
In some unusual cases, the same solution can be derived inductively, and deductively. This is illustrated with the following example. 2, 4, 16, Y. Y equals the unknown number in the sequence. In addition, the sum of the four numbers, including Y, is 278. That is 2+4+16+Y=278. What is the value of Y.
The inductive solution is based on observation, which resulted in the,
following hypothesis: ![]() Thus, S=16, and Y=next number
in sequence.
Thus, S=16, and Y=next number
in sequence. ![]() The
Conclusion is Y=256 or 2, 4, 16, 256
The
Conclusion is Y=256 or 2, 4, 16, 256
The above solution can be devised with deductive reasoning by using algebra, as follows. The given is the sum of all the numbers in the sequence, including Y, is equal to 278. Thus, 2+4+16+Y=278. Then 22+Y=278, and Y=278‑22 Thus, the conclusion is Y=256. Thus the sequences is: 2, 4, 16, 256
____EXAMPLE 4____
Usually, deductive reasoning is based on the observation or evaluation of a relatively small number of samples of a very large set, or population. However, if you are dealing with a set, or population, that consists of a relatively small number of entities, you can observe or evaluate every entity, to derive your conclusions. In such a case, the conclusion should be as accurate as deductive reasoning. This applies to observations or evaluations of small groups, such as students in a classroom, or the employees of specific organization.
See the Following Websites From Other Authors for Additional Information, and Alternative Perspectives on Logical Thinking and Related Concepts
TEN VIDEOS
1) Video “Inductive Reasoning - Concept”, 2) Video “Episode 1.3: Deductive and Inductive Arguments“, 3) Video “Deductive and Inductive Arguments“, 4) Video “1.1 Basic Concepts: Arguments, Premises, & Conclusions, 5) Video, The limits of computer logic, Morten Rand-Hendriksen, 6) Video, Fuzzy Logic: An Introduction, IEEE Computational Intelligence, Society IEEE Computational Intelligence Society, 7) What is Fuzzy Logic? - Professor Bob John, 8) Lotfi Zadeh and Fuzzy Logic, 9) Fuzzy Logic and Beyond - A New Look by Lotfi Zadeh - Workshop on Fuzzy Logic, 10) Logic and Set Theory
ARTICLES ON WEBSITE
1) Ontologies and Logic Reasoning as Tools in Humanities?, 2) The psychology of moral reasoning, Monica Bucciarelli, University of Turin, 3) Some uses and limitations of fuzzy logic in artificial intelligence reasoning for reactor control, Michael A.S. Guth, 4) Logical Varieties in Normative Reasoning, Mark Burgin Kees (C.N.J.) de Vey Mestdagh, 5) Abductive reasoning: Logic, visual thinking, and coherence, Paul Thagard and Cameron Shelley, 6) The Limits Of Logic, Brian D. Rude, 1974 , 7) WHAT IS THE DIFFERENCE BETWEEN REASON AND LOGIC? HOW RELIABLE IS INDUCTIVE REASONING? ARE WE PREDICTABLY IRRATIONAL?, 8) Tutorial L01] What is logic?, , 9) DEFINITION
fuzzy logic, 10) THE FUZZY WORLD
To go to the first page of this
chapter left click on these words.
Below is the hyperlink table of contents of this e-book. If you Left click on a specific: chapter, section, or subsection, it will appear on your computer screen. Note the red chapter headings, the yellow highlighted sections, and the blue subheadings are all active links.
Reasoning: Introductory Concepts
Reasoning for Comprehension, and Reasoning for Solving Problems, and Creating Entities
Visual Reasoning, and Related Concepts
Visual Reasoning for Comprehension, & Problem Solving
Verbal Reasoning and Related Concepts
Verbal Reasoning for Comprehension, & Problem Solving
Verbal Reasoning, and Logical Statements
Verbal Reasoning: Two Categories of Logical Statements
Mathematical Reasoning, and Related Concepts
Mathematical Reasoning for Comprehension, And Problem Solving
Reading and Learning Mathematics
Mathematical Reasoning in General
Deductive & Inductive Reasoning, with Related Concepts
Introductory Note on Variations in the Descriptions of Deductive and Inductive Reasoning
Deductive Reasoning, with Verbal and/or Visual Reasoning.
Writing, with an Informal Deductive Reasoning Structure
Conclusions From Deductive Reasoning Can Sometimes Be Converted To Definitions That Are Indisputable
Checking the Validity of Inductive Reasoning
Checking Inductive Reasoning in Everyday Life
Can Inductive Reasoning Be as Precise as Deductive Reasoning?
Logical Thinking and Related Concepts
To go to the first page of this
chapter left click on these words.
If you want to go to the next chapter
left click on the link below
www.TechForText.com/SL/Chapter-7
If you want to see a list of all
the chapters in this e-book go to