The‑Tangent‑Cotangent-Integral-Calculus-Generator
A software based calculation device to help students practice solving trigonometric integrals
Created by David Alderoty © 2011, e-mail David@TechForText.com
To contact the author use the above email address or
left click on these words for a website communication form.
This website provides, free of charge, the Tangent-Cotangent-Integral-Calculus-Generator, which is a software based calculation device, designed to help students practice solving trigonometric integrals. This software is available for download in JavaScript, Microsoft Excel, and OpenOffice Calc, formats. In addition, there is an online version of the Tangent-Cotangent-Integral-Calculus-Generator, embedded in this webpage, three paragraphs below. (The Excel and OpenOffice Calc versions require Microsoft Windows. The online and downloadable JavaScript versions will function with any modern operating system, but it was only tested with Windows.)
If you want to download the Tangent-Cotangent-Integral-Calculus-Generator, or want additional information, scroll all the way down, beneath the online version. Alternatively, you can go to the table of contents of this website, by left clicking on these words. If you want to go directly to the download section left click on these words. If you want to go directly to the instructions for the Tangent-Cotangent-Integral-Calculus-Generator, left click on these words. You should read the instructions before using this software. If you want an online printer friendly version of the Tangent-Cotangent-Integral-Calculus-Generator left click on these words.
The Tangent-Cotangent-Integral-Calculus-Generator provides integral problems that involve tangent and cotangent. I created a similar device for integral problems involving sine and cosine called the Trig-Integral-Calculus-Generator, which is located on another website: www.TechForText.com/Trig-Integral-Calculus-Generator With a few exceptions, the instructions, technical material, and other descriptive text, on both websites are almost identical. Thus, if you read the instructions, and other material on the above website, and retain the information you need, it is not necessary to read the text on this website.
Downloads and Related Information for the Tangent‑Cotangent Integral‑Calculus‑Generator
Step 1) Left click with the mouse on a blue download *link, for the Tangent-Cotangent-Integral-Calculus-Generator and a dialog box will open, with an option to save the file. *Note the download links are located in the next subsection.
Step 2) Save the file on the Windows Desktop or in the Documents Folder, or anywhere else on your computer, where you can easily locate the file’s icon. Keep in mind that after you downloaded the file, you must locate the file's icon on your computer.
Step 3) The file's icon can be moved after downloading to any location on your computer, with the windows cut and paste function. You should move the icon to a location on your computer where you can easily find it. For most people, the best place to store these files is in the Documents Folder (also called the My Documents in some versions of Windows).
An alternative to the above three steps, is to download the Tangent-Cotangent-Integral-Calculus-Generator in a zipped folder. To do this left click on a link with the words: zipped folder. With this method, most browsers display the files icon as soon as the download is completed. Then you can use the Windows cut and paste function, to place the file anywhere you want on your computer.
If you need additional information on downloading, left click on the Google search link, below:
Google Search:[How to download files from the Internet]
Download Links, for the Microsoft Excel Format
If you want the above in a zipped folder, left click on these words.
If you want the above in a zipped folder, left click on these words.
If you want the above in a zipped folder left click on these words.
Download Links, for the OpenOffice Calc Format
If you do not have Microsoft Excel on your computer, the best alternative is to use OpenOffice Calc, for the Tangent-Cotangent-Integral-Calculus-Generator. To do this, you must first obtain the FREE OpenOffice.org software package, which provides almost the same functionality as Microsoft Excel, Word, PowerPoint and Access. The OpenOffice.org software package is open-source, and you can download it from the following website: www.OpenOffice.org
Download Links, for the JavaScript Version
If you do not have Microsoft Windows on your computer, you can use the JavaScript version of the Tangent-Cotangent-Integral-Calculus-Generator. The JavaScript version should work with most modern operating systems, but it was only tested with Windows.
The following two JavaScript versions are in the Web Archive, Single file, format, and they were converted to this format with the save function in Internet Explorer. This file format is different than the conventional HTML, and it has the extension .mht. The primary advantage of this file format is it combines the graphics and computer code into one file. With conventional HTML, the graphics can easily get disconnected from the file, if it is not carefully stored in one folder. Web Archive, Single file is supported by most of the popular browsers, such as Firefox, Chrome, and Opera, but I was unable to open this file format with SeaMonkey, version 2. It will be easier to download the following two JavaScript files, in a zipped folder, if you are not familiar with the save function in your browser.
If you want the above in a zipped folder, left click on these words.
If you want the above in a zipped folder, left click on these words.
Download Link, for All of the above, in One Zipped Folder
General Description and Instructions
Software and Computer Requirements for the Tangent‑Cotangent-Integral‑Calculus‑Generator
All the versions of the Tangent-Cotangent-Integral-Calculus-Generator, are less than 1 MB. Thus, this software requires very little computer resources, and it should function well even with the older computers. However, the Excel and OpenOffice Calc versions of the Tangent-Cotangent-Integral-Calculus-Generator, require Microsoft Windows. The online version and the downloadable JavaScript version should work with any modern operating system, providing it has an Internet browser that supports JavaScript. Almost all browsers currently available provide the needed JavaScript functionality, to operate the Tangent-Cotangent-Integral-Calculus-Generator. Thus, the online and JavaScript version should work with Macintosh, and Linux, with a JavaScript enabled browser, but it was only tested with Microsoft Windows.
The Primary Purpose, of the Tangent‑Cotangent-Integral‑Calculus‑Generator
The Tangent-Cotangent-Integral-Calculus-Generator is designed for students that know the basic method of solving a trigonometric integral, but need practice to avoid errors, and to increases speed and efficiency with these calculations. The Tangent-Cotangent-Integral-Calculus-Generator is not designed to teach trigonometry or calculus, or to explain related mathematical principles. If you need this type of instruction, you should carry out Google searches for VIDEOS for calculus, trigonometry, and for solving trigonometric integrals.
Functionality and Description of the Tangent‑Cotangent-Integral‑Calculus‑Generator
The Tangent-Cotangent-Integral-Calculus-Generator generates twelve math problems, involving trigonometric integrals, based on two numbers entered by the user. These numbers are for two angles, designated as B and A, and they appear on each integral as illustrated in the following example:
Angle B is on the top

Angle A is on the bottom
With this example, the user entered 0.5pi radians (90 degrees) for angle B, and 0.25 pi radians (45 degrees) for angle A. (Note, the above illustration is an actual copy of an integral from the Excel version of the Tangent-Cotangent-Integral-Calculus-Generator)
Based on the above illustration, when angle B is greater than angle A the calculated results will generally be positive, and when angle A is greater than angle B results will be negative. This is assuming that positive angles are entered, that are less than 90 degrees, but greater than 0 degrees.
The angles that are entered in the input boxes of the Tangent-Cotangent-Integral-Calculus-Generator, should generally be greater than 0 degrees, but less than 90 degrees. If this is not done, some of the integrals will not have any calculated results. However, the calculation mechanism in this software can perform calculations, with very large and very small numbers, which may be positive or negative.
When the user (student) enters numbers, for angles B and A, the software instantaneously calculates the results for the twelve integrals. However, these results are initially concealed from the user.
The student’s job is to try to solve
each integral with pencil and paper, and a calculator for the arithmetic and
trigonometric functions. After attempting to solve each integral, the user
checks his/her calculations, with the results calculated by the software.
To do this there is a pull-down menu, highlighted in pink, under each
integral. The user left clicks on this menu, and moves it down one
level, and the calculated results are displayed. This mechanism is
designed to reveal the results for one integral at a time.
There are input boxes on the top of the Tangent-Cotangent-Integral-Calculus-Generator, where the user enters numbers for angles B and A. The numbers can be entered in either degrees or radians. When degrees are used, the numbers must be entered in the right input boxes, and when radians are used the numbers must be entered in the left input boxes.
When radians, are used with the Tangent-Cotangent-Integral-Calculus-Generator, the angles are entered in terms of fractions or multiples of pi. Examples are, if you enter 2, it is NOT two radians; it is 2pi radians, which is equal to 360°. If you enter 1, it is not one radian it is 1pi radians, which is 180 degrees. If you enter 0.5 it is 0.5pi, which is equal to 90°, etc.
I designed the above functionality into the software, because it simplifies the process of entering angles in radians. For example, if you entered one revolution of a circle, or 360 degrees, in radians, using the conventional method, you would have to enter 6.283185307 radians. For one half of a revolution (or 180 degrees) you would enter 3.141592654 radians, and for one quarter of a revolution (or 90 degrees) you would enter 1.570796327 radians, etc. However, with the mechanism I built into this software, when you enter a number in the input box for radians, it is multiplied by pi. This means when 2 is entered it is 2pi radians (or 360 degrees), when 1 is entered it is 1pi radians (or 180 degrees), etc.
Just under the input boxes there are two display boxes that show the angles that were entered by the user in both degrees and radians. Thus, regardless of what the user enters, the display boxes will perform the necessary calculations to display both degrees in radians. For example, if you enter 45°, the display box will show the following:

Just like the display boxes, discussed above, the angles on the integrals are displayed in both pi radians and degrees, as illustrated in the following diagram:

Scientific Notation and the Tangent‑Cotangent-Integral-Calculus-Generator
The Tangent-Cotangent-Integral-Calculus-Generator may display very large and very small calculated results in scientific notation, using the letter e. (The Excel version uses a capital E) An example of a large number in this format is:
4.4218961132108144e+116.
An example of a very small number displayed in this format is:
2.5746740266666662e-130
Extremely small numbers, such as the above might be rounded to zero by the software, because they are generally considered insignificant.
If you want to see very small numbers, in your calculated results, for whatever reason, there is a control mechanism on the upper portion of the Tangent-Cotangent-Integral-Calculus-Generator, for setting the number of decimal places that are displayed. The default is 5 decimal places. Change this number to 300, which will totally eliminate the rounding function.
The Tangent-Cotangent-Integral-Calculus-Generator is Very Easy to Use, as Explained in the Following Four Steps.
Step 1) Enter any two numbers you prefer for angles B and A, in the white input boxes, on the top of the Tangent-Cotangent-Integral-Calculus-Generator. (It is best to enter numbers that are less than 90 degrees, but greater than 0 degrees. If this is not done some of the integrals may not have calculated results.) You can enter the angles in degrees or radians. *If you want to enter the angles in radians use the input box on the left, but if you want to enter the angles in degrees use the input box on the right. It is probably easier to enter the angles in degrees, if you do not want to deal with decimals.
With the numbers you enter, the software generates twelve math problems, involving trigonometric integrals, which you are to solve. The software calculates the solution to each of these problems automatically, but the results are initially concealed.
*Note When angles are entered in radians, with this software, they are entered in terms of a fraction or multiple of PI. Examples are if you enter 2, it is NOT 2 radians, it is 2pi radians,(= 360 degrees); if you enter 1, it is NOT 1 radian, it is 1pi radians, (= 180 degrees); if you enter 0.5 it is NOT 0.5 radians, it is 0.5pi radians (= 90 degrees).
Step 2) After entering the numbers in the white input boxes, scroll down and you will see twelve trigonometric integrals, which progressively increase in difficulty. Your job is to try to solve each integral with pencil and paper. To do this, you should have a list of the formulas needed to solve the integrals, and a scientific calculator.
A list of the formulas you need for the calculations is on this website, under the following heading:
A List of Formulas to Help You Solve the
Math Exercises Generated by the
Trig Integral Calculus Generator
To go directly to the List of Formulas left click on these words
If you do not have a handheld calculator, with trigonometric functions, you can use the calculator provided with the Microsoft Windows operating system. The Windows calculator has a setting for a scientific calculator, and when it is set, the trigonometric functions are displayed on the keypad of the calculator. With the version of Windows that I am working with, (Windows 7), the view menu (on the calculator) has the setting for the scientific calculator.
Another alternative is to use an online scientific calculator. Links to three of these calculators are provided below:
http://www.calculateforfree.com/sci2.html
http://calculator.pro/Scientific_calculator_online.html
Step 3) After attempting to solve each integral, check your calculations, with the software. To do this, there is a pink pull-down menu, below each integral, to display calculated results. A picture of the menu for the online and downloadable JavaScript versions of the Tangent-Cotangent-Integral-Calculus-Generator is presented below:
![]()
Left click anywhere on the menu, and it will open. Then scroll down one level, until you see the words: The Calculated Result, Displayed Above in Red Type. Left click on these words, and the menu will close. If the above was carried out successfully, the menu will appear as follows, with the calculated results above it.
![]()
The menus in the Excel and OpenOffice Calc versions, of the Tangent-Cotangent-Integral-Calculus-Generator, are slightly different than the above. A picture of this menu is presented below:
![]()
To open this menu, it is necessary to left click once on the pink section, and again on the right section with the red cross. When this is done, the menu opens, and as with the JavaScript version, move downward one level, to the words The Calculated Result, Displayed Above in Red Type. Than Left click on these words (The Calculated Result, Displayed Above in Red Type).
Step 4) For each practice session, change the numbers in the white input boxes, if you want a set of twelve integrals that have calculated results that are different than the integrals in your previous practice session. Keep in mind that multiple practice sessions are usually required to master a mathematical technique.
Trigonometric Integral Formulas, And Related Concepts
This section provides information about integral formulas that relate to the Tangent-Cotangent-Integral-Calculus-Generator. This includes a list of the formulas, to help you solve the integral problems generated by this software. Tangent-Cotangent-Integral-Calculus-Generator. These formulas are indefinite integrals. Some of these formulas are frequently illustrated in calculus classes and in mathematics books.
The Source: for the Integral Formulas Listed in This Section
The integral formulas listed in this section, were
actually calculated by commercially available mathematics software, in
symbolic notation. This may sound strange to some of us, but
modern mathematics software, can carry out calculations without numbers, to
generate formulas. For example, I entered:![]()
![]() , and the software calculated
, and the software calculated ![]() .
.
However, the formulas calculated by the mathematics software are available from conventional reference sources dealing with calculus and trigonometry. Nevertheless, some of the formulas presented in this section might be structured with trigonometric equivalents that are different then the formulas you have in your reference sources, or the formulas you are familiar with.
I simplified some of the formulas calculated by the mathematics software, such as by adding several terms together into one fraction. When this is the case, I present the formula calculated by the software first, followed by the formula with my modifications.
The mathematics software failed to calculate a constant, which is usually represented by the letter C, in all of the sources I have seen with indefinite integrals. I corrected this with all of the formulas. However, the C is not relevant for the problems that are generated by the Tangent-Cotangent-Integral-Calculus-Generator.
Constant at the End of Indefinite Integrals
The above raises the question, why
are constants placed at the end of an indefinite integral, such as ![]() The answer to this
question becomes obvious, if you think of the formulas as
anti-derivatives. When you take a derivative constants are calculated as
zero. A simplified example involves taking the derivative of the
following:
The answer to this
question becomes obvious, if you think of the formulas as
anti-derivatives. When you take a derivative constants are calculated as
zero. A simplified example involves taking the derivative of the
following: ![]() , which equals
, which equals ![]() . Now, if we attempt to reverse
the procedure, by taking the anti-derivative of 6X, (without including a C at the end of the calculation) we get:
. Now, if we attempt to reverse
the procedure, by taking the anti-derivative of 6X, (without including a C at the end of the calculation) we get:
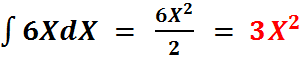 We did not obtain
the original expression, when we reverse the procedure. When a
derivative of an expression is taken, information is lost as a result of the
calculation. To represent this potential or actual loss of information the
anti-derivative can be calculated as
We did not obtain
the original expression, when we reverse the procedure. When a
derivative of an expression is taken, information is lost as a result of the
calculation. To represent this potential or actual loss of information the
anti-derivative can be calculated as ![]() The C can represent any value, and with the above
example we know that it represents 10.
The C can represent any value, and with the above
example we know that it represents 10.
Creating the Spreadsheet Formulas, with the Indefinite Integrals, to Create the
Tangent-Cotangent-Integral-Calculus-Generator
The Tangent-Cotangent-Integral-Calculus-Generator, was initially created in Microsoft Excel, then it was electronically converted to OpenOffice Calc, and JavaScript. The OpenOffice Calc conversion was carried out with OpenOffice Calc software, and the conversion to JavaScript was performed with SpreadsheetConverter.
Thus, I had to create twelve spreadsheet formulas, one for each integral, which would function in Microsoft Excel. To do this, I used the list of indefinite integrals presented below. The basic idea of how this was done, can be illustrated with:
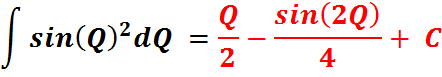
Note: The formula I am using to illustrate the following steps, was not used in the Tangent-Cotangent-Integral-Calculus-Generator. The steps presented below are presented to explain general principles. Many details are left out, to provide a brief and clear explanation.)
Step 1) The indefinite integral 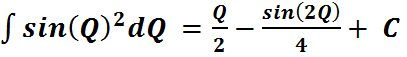 was simplified by combining the
fractions, which resulted in
was simplified by combining the
fractions, which resulted in
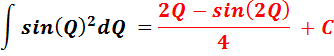
Step 2) An integral based on the above, was written and solved in terms of angles B and A. This resulted in the following:
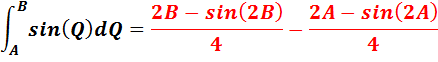
Step 3) The result was simplified by adding the two fractions together, which resulted in the following:

Step 4) A spreadsheet formula was created with the above. For the spreadsheet formula, we only need the expression to the right of the equal sign, illustrated in red type above. For spreadsheet formulas a / is used for division, and when there is more than one term involved ( )/. When the above formula is rewritten with ( )/ we get:
![]()
Step 5) The white input boxes, were renamed as B and A, with the renaming functionality, available in Microsoft Excel. Before these input boxes were renamed, they had default cell designations as names.) With the renaming technique I used, Microsoft Excel can interpret the meaning and value of B and A, by the numbers that are entered in the white input boxes, and calculate with the formula:
![]()
Without the above renaming procedure,
Excel cannot interpret the meaning or value of B and A,
and cannot calculate with any formula written with these letters.
From the above, it is probably obvious that the spreadsheet versions of the integral formulas do NOT look like the conventional mathematics used to solve integrals. However, they are in fact mathematically equivalent, but the notation used to write spreadsheet formulas is different than the conventional way of writing mathematical expressions.
If you want to see the spreadsheet formulas that I created for the Tangent-Cotangent-Integral-Calculus-Generator, look under each integral, when the calculated results are displayed. You will see the words spreadsheet formula followed by the formula. When a spreadsheet formula is excessively long, the words spreadsheet formula is abbreviated. (Note when a calculated result is concealed by the Tangent-Cotangent-Integral-Calculus-Generator, the related spreadsheet formula is also concealed.)
A List of Formulas to Help You Solve the Math Exercises Generated by the Tangent-Cotangent-Integral-Calculus-Generator
The formulas listed below are presented sequentially, to coincide with the numbering for each problem on the Tangent-Cotangent-Integral-Calculus-Generator.
Note: some of the formulas listed below involved natural logarithms, which are represented by ln, or more precisely ln( ). For example:
ln( 4 )=1.386294361
__________________________________
Needed For Problem 1
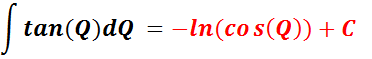
__________________________________
Needed For Problem 2
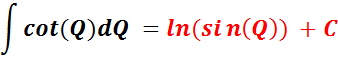
__________________________________
Needed For Problem 3
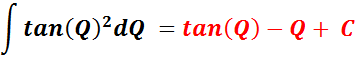
__________________________________
Needed For Problem 4

__________________________________
Needed For Problem 5

__________________________________
Needed For Problem 6
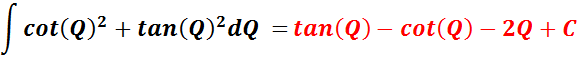
__________________________________
Needed For Problem 7
![]()
__________________________________
Needed For Problem 8
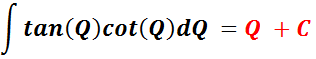
__________________________________
Needed For Problem 9
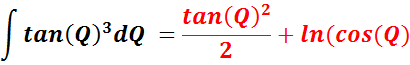
__________________________________
Needed For Problem 10
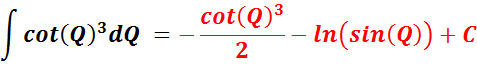
__________________________________
Needed For Problem 11
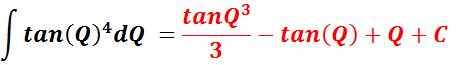
OR
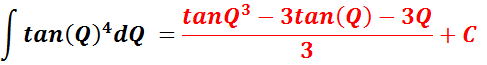
__________________________________
Needed For Problem 12
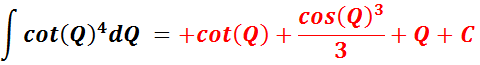
OR
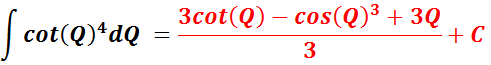
__________________________________
The Design Concepts, and Services Offered by the Author
Design Concept to Maximize User‑Friendliness: For the Website and For The Tangent-Cotangent-Integral-Calculus-Generator
I designed the Tangent-Cotangent-Integral-Calculus-Generator, and this website, in a way that would maximize efficiency and ease-of-use. The Tangent-Cotangent-Integral-Calculus-Generator has instructions placed next to related input cells, and it is laid out with a simple structure, with large fonts. The website similarly has large fonts, with a similar structure, and clearly written instructions. For example, the download links on this website contain precise wording, to prevent confusion, such as: If you want the Tangent-Cotangent-Integral-Calculus-Generator in the Excel format, left click on these words.
The website is on one long webpage. This provides the convenience of scrolling down or up, from one section to another, and it avoids the unnecessary complexity of pull-down menus, and links to go from one page to another. However, I provided a hyperlink table of contents as an alternative way of navigating the website.
Some of the material on this website is technical. Thus, for an optimum level of comprehension, the reader IDEALLY should have an advanced background in spreadsheets software, coupled with knowledge of programming concepts and calculus. However, I structured each sentence with the goal of minimizing confusion, and maximizing comprehension, for users with varying levels of technical knowledge. In this regard, perfection is never possible, because users come from diverse technical, cultural, and linguistic backgrounds.
I provided many headings and subheadings throughout this text. This allows the user to easily skip material that they find difficult, or uninteresting. The headings and subheadings are also displayed in the table of contents.
Services Offered by the Author David Alderoty
I design and build user-friendly software based calculation devices for arithmetic, accounting, currency exchange rates, algebra, trigonometry, correlations, calculus, and databases with built-in calculation devices. I also create attractive online calculation devices for websites. I generally make these devices in the Microsoft Excel, OpenOffice.org, and the JavaScript formats, but I can work with other spreadsheet formats besides the above. I also create web communication forms in JavaScript for websites. This includes forms with built-in calculation devices. For a list of websites with calculation devices that I created, left click on these words, or go to the following website: www.TechForText.com/Math
I write instructions for the devices I build. I can also write instructions for software and computer devices created by others. In addition, I can write advertising for your websites, products and services.
I can provide the services mentioned above on a fee-for-service basis, or possibly based on temporary or permanent employment. If you are interested in my services, and want additional contact information or more data on the services I offer, you can email me at David@TechForText.com or use a website communication form, by left clicking on these words.
For a list of all the services I offer see www.TechForText.com For a list of all my websites see www.David100.com My resume is online at: www.David100.com/R
My name is David Alderoty, and I am located in the USA, New York City. If you are a great distance from my locality or are in another country, this is not important. I can provide the above services worldwide, because the software and the writing services I offer can be delivered through the Internet to any locality, providing there are no governmental restrictions.

Introduction to The Hyperlink Table of Contents of this Website
This website is more or less laid out like a book, but it is on one long webpage. You can scroll up or down to go from one topic to another. However, if you want to examine all the sections and subsections of this website, use the hyperlink table of contents, below this paragraph. To go to any section or subsection of this website you can left click on the blue words that relate to the material you want to read. The yellow highlighted words are sections, and the un-highlighted words are subsections.
If you want to go to the top of the website, left click on these words.
Table of Contents of this Website Contents
The‑Tangent‑Cotangent-Integral-Calculus-Generator 1
Downloads and Related Information for the Tangent‑Cotangent Integral‑Calculus‑Generator 20
Three Steps for Downloading. 21
Download Links, for the Microsoft Excel Format 23
Download Links, for the OpenOffice Calc Format 25
Download Links, for the JavaScript Version 26
Download Link, for All of the above, in One Zipped Folder 30
General Description and Instructions. 31
Software and Computer Requirements for the Tangent‑Cotangent-Integral‑Calculus‑Generator 31
The Primary Purpose, of the Tangent‑Cotangent-Integral‑Calculus‑Generator 33
Functionality and Description of the Tangent‑Cotangent-Integral‑Calculus‑Generator 34
Scientific Notation and the Tangent‑Cotangent-Integral-Calculus-Generator 41
Trigonometric Integral Formulas, And Related Concepts. 50
The Formulas: Introduction. 51
The Source: for the Integral Formulas Listed in This Section. 52
Constant at the End of Indefinite Integrals 54
Creating the Spreadsheet Formulas, with the Indefinite Integrals, to Create the. 56
Tangent-Cotangent-Integral-Calculus-Generator 56
The Design Concepts, and Services Offered by the Author 66
Services Offered by the Author David Alderoty 69