The Theorem Of General And Universal Equations, For Creating Generalized Equations, With The Formulas From Mathematics And Physics Created by David Alderoty
The Theorem Of General And Universal Equations,
For Creating Generalized Equations, With The
Formulas From Mathematics And Physics
Created
by David Alderoty © 2012
David@TechForText.com
To contact the author use the above e-mail address, or
left click on these words for a website communication form
This website is a 5300 word e-book
The theorem and related concepts presented on this website have practical and theoretical utility, for all of the following:
For simplifying mathematical calculations
For developing a better understanding of the formulas from physics and mathematics
For facilitating creative thinking, which can lead to new theories and concepts
Facilitates the understanding of formulas, which can help with the learning process.
*For creating software-based calculation devices
*With the Theorem of General and Universal Equations I created three computer programs that perform multiple calculations simultaneously. These devices function online over the Internet, and they can be accessed from the following URLs: (NOTE the blue words in this book are active hyperlinks, and you can left click on them to open the indicated webpage.)
www.TechForText.com/General-Area-Equation
www.TechForText.com/General-Volume-Equation
Physics Calculator for Molecular Speed
I devised the theorem and concept discussed in this e-book several years ago, and the following material represents a simplified an updated version of an e-book I placed online in 2009. I have recently edited the original e-book and moved it to the URL presented below. The original e-book is slightly more technical, and it contains some material that is not presented on this website.
The theorem and related material discussed on this website, and the older e-book mentioned above, require a working knowledge in mathematics and physics. The primary focus of both of the e‑books is on mathematics and physics, but it is important to note that the theorem, and related techniques can be applied to just about any discipline that utilizes mathematical equations.
NOTE ON THE TERMINOLOGY USED IN THIS E-BOOK
The words UNIVERSAL EQUATION, means in this paper a GENERALIZED EQUATION that applies to MANY or ALL calculations in a specific set or category, such as a formula that represents the area calculations of many or all geometric figures. A GENERAL EQUATION means any equation that applies to two or MORE calculations in a specific category, such as a generalized formula for volume that can be used to calculate the volume of cubes and spheres. The word formula(s) and equation(s) are used as synonyms in this e-book.
Section 1) Introduction
Over the years, mathematicians and physicists have tried to find coefficients that are universal in nature, which are generally called universal or fundamental constants, such as pi, Euler's number, Planck's constant, the gravitational constant, and the speed of light. These numbers have theoretical and practical value in a number of formulas. However, my paper takes the OPPOSITE APPROACH, which in NO way contradicts the conventional concepts of physics and mathematics. Specifically, the constants I use are NOT universal, and more precisely should be called coefficients, but THE EQUATIONS I DERIVED ARE UNIVERSAL. Of course, the *universal equations provide the same calculated results as the conventional mathematics and physics formulas.
The above suggests the question: Why Create Universal Equations?: The answer is universal equations provide a look at the principles and concepts of physics and mathematics from a unique perspective. This is similar to looking at an object from a different angle, which might reveal new information, insights and theories. Universal equations generally convey precise principles, which can result in a better understanding of the conventional formulas and concepts of physics and mathematics. The generalized equations are sometimes useful for deriving new formulas and they are often more versatile than conventional formulas. Sometimes, a universal equation is useful for carrying out calculations that cannot be done with conventional formulas. All of this will become apparent in the next section, which presents a simplified derivation of a general area formula.
Section 2) A Simplified Illustration Deriving A Universal Area Formula With The Theorem Of General Equations
Section 2) A Simplified Illustration
Deriving A Universal Area Formula
With the Theorem of General Equations
To explain the basic idea of my thesis in a simplified way, I will create a universal area formula, and I will illustrate this step-by-step. To do this I will start with six conventional area formulas, with the goal of creating ONE FORMULA that represents area of two-dimensional geometric figures, as well as the surface area of three-dimensional objects. In this regard, the first step is to examine the six area formulas presented below, and then proceed to the next paragraph, which is below the formulas.
(THE AREA OF A RECTANGLE) A = LW The area = A of a rectangle, is equal to the length=L multiplied by width=W (The coefficient is 1 and the two lengths are L and W)
(THE AREA OF A TRIANGLE)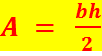 
(The area = A of a
triangle, equals base=b
multiplied by height=h,
divided by 2 (The coefficient is ½ The two
lengths are b and h)
(THE AREA OF A SQUARE) 
The
area = A of a square, equals the length of the
side = S squared (The coefficient is 1 and the two lengths
are S and S)
(THE SURFACE AREA OF A CUBE) 
(The
surface area = A of
cube, equals the length of the side = S squared multiplied by 6) (The coefficient is 6
and the two
lengths are S and S)
(THE AREA OF A CIRCLE) 
The
area of a circle area = A,
equals 
multiplied
by the radius squared (The coefficient is 
and the two lengths are
r
and r)
(THE SURFACE AREA
OF A SPHERE) 
The
surface area = A of a
sphere, equals 4 times multiplied
by the square of the radius. (The coefficient is 
and the two lengths are
r
and r)
If you examined the six area formulas presented above, you may have noticed that they all have two lengths multiplied together. This essentially involves the length of two line segments, or distances, multiplied together, which is multiplied by a coefficient that relates to a specific geometric figure. The line segments that are multiplied together are usually perpendicular to each other, with most area formulas. This can easily be seen in one of the simplest cases, which is the formula for calculating the area of a rectangle, which is length multiplied by width or A = LW. We can represent the two lengths of all of the formulas presented above with Lg and Wg. I am representing the areas of all the formulas with: Ag. These representations are defined concepts, and thus they are true by definition.
If you
examine the six area formulas once again, you will notice they
all have a
constant or coefficient. For example, the area of a
rectangle has a coefficient
of: 1, for the area of a
circle it is: 
,
and for the surface area of a sphere
it is: 
.
We can represent all of these coefficients
with KA
The resulting concept,
KA,
is defined and it is true by definition.
(NOTE:
A logical choice is to use c, for the coefficients, but c is
used in this
e-book, and in many other books on physics, to represent the
speed of light, so
I am using the letter K to prevent confusion. Actually,
another good
alternative is to use an uppercase C to represent the
coefficients.)
With the above information we can create a general area formula. That is area involves two lengths multiplied together, (LgWg) multiplied by a coefficient (KALgWg). Thus, Ag = KALgWg is our universal or general area formula. The mathematical relationship represented by this formula (Ag = KALgWg) are based on defined concepts, and the formula is true by definition.
If we want to
actually use this formula to perform calculations, we must
know the value of KA
for our geometric figure. For example, if we want to
find the area of a circle
it is obvious that KA = , and we know that the two
lengths are Lg = r
and Wg = r.
However, if we want to use this to calculate the
surface area of a sphere, KA =
and Lg = r and Wg = r. For rectangle, obviously, KA = 1 , Lg = the length and Wg = Width.
I have created a software-based calculation device using the General Area Formula discussed above. This software functions online, over the Internet, and you can access it from the URL presented below:
www.TechForText.com/General-Area-Equation
Section 3) The Theorem of General and Universal Equations
Section 3) The Theorem of
General and Universal Equations
If you understand the above example (of how Ag=KALgWg was derived) you should have no difficulty in understanding the following. However, if you did not understand the above, you should reread the material, and carry out some calculations with pencil and paper to facilitate understanding of the ideas before reading the following:
AN ESSENTIAL NOTE: It is important to keep in mind that the value of the K terms are determined by the specific nature of the calculations, with the above theorem, and with any other technique used in this e-book to derive general equations. That is by definition K represents the multiplier (a coefficient) that will yield the correct calculated results. If you derive any value for a K term that does not produce the correct calculated results, you have an INCORRECT value of K, which is true by definition. If you do not understand the above, reread it, because it is essential for understanding the mathematical derivations presented in this e‑book.
There is another important concept to keep in mind that relate to the above theorem, and many of the techniques presented in this book. Specifically, the value of the K term is sometimes partly determined by the units that are used in a formula. For example, if we calculate the area of a square, the value of K is 1, as previously explained. However, if we want to use feet for the measurement, but we want the calculated result in square inches, the value of K is not 1. Actually, with this example K = 144. This will be clarified with the following example:
Let us assume that the square measures 1.5 feet, then the calculation would be (144)(1.5)(1.5) = 324 square inches. Thus, by using the appropriate value for K it is possible to create formulas, and software-based calculation devices, that calculate using mixed units, such as meters and centimeters, or even inches and meters.
Using some of the concepts described above I created a calculation device that uses the same formula, with a number of values for K, to calculate the speed of gas molecules, at a specific Kelvin temperature. Specifically, this software calculates SIMULTANEOUSLY: Root Mean Square Speed, Average Speed, The most Probable Speed, and The Average Of The Three Speeds Mentioned Above. In addition the calculations are presented in meters per second, kilometers per second, feet per second, and miles per hour. This calculation device functions online, over the Internet, and you can access it by left clicking on the following link.
Physics Calculator for Molecular Speed
Sometimes, a formula is needed that calculates a quantity that does not relate directly to the variables in the formula. This idea can be clarified with the following examples.
If you are selling real estate, you may want to calculate the selling price of a property, based on the number of square feet. This can be calculated directly as follows.
Assuming, the calculations are based on a rectangle, the value of K would equal the price per square foot. Let us assume that the land measures 50 feet by 100 feet, and it is selling for $100 per square foot. With this example the value of K = $100, and the calculation is presented below:
$100(50)(100) = $500000.
A more complex example
similar to the above involves
real estate that is circular in shape, and has a radius of
50 feet, and also
sells for $100 per square foot. In this case the value
of the K = 
,
and the calculation is as follows:
Another example, using the above concept is calculating weight, based on height, length, and width. For example, if a foundation measuring 100 feet, by 100 feet, with a depth of 40 feet must be created to erect a building, what is the weight of the material that must be removed. Let us assume that the average weight of the material is 100 pounds per cubic foot, and we want to know how many tons must be removed to create the foundation. With this example the value of K is 0.05 (The value for K is based on 2000 pounds for one ton, which results (100/2000) = 0.05). The calculations for the foundation are as follows:
(0.05)(100)(100)(40)=20,000 tons
Section 4) Modifying a General Equation So It Will Apply To a Larger Number of Cases
Section 4) Modifying a General Equation
So It Will Apply To a Larger Number of Cases
es
Sometimes a general formula can be further modified, so it will apply to a larger number of cases: To explain precisely what this means I will return to the previous example of the general area formula. That is the formula derived above Ag = KALgWg applies to most, if not all area and surface area calculations. However, in some cases it will involve the calculation of separate areas of a geometric figure, which are added together, to gain the total area. This applies to, two and three-dimensional geometric forms that are comprised of two or more geometric figures, such as a cardboard box or a building with a dome shaped roof. If the geometric figures that comprise the geometric form differ, the value of KA will differ. This applies to the surface area calculations for the example given above, a building with a dome shaped roof. The general area equation can be Ag=KALgWg can be modified slightly so that it applies to the geometric forms mentioned above, as follows:
Starting with three, or more general area formulas:
Ag1=KA1Lg1Wg1, Ag2=KA2Lg2Wg2, Ag3=KA3Lg3Wg3
Addition: Ag1+Ag2+Ag3 = KA1Lg1Wg1+KA2Lg2Wg2+KA3Lg3Wg3
and if Ag1+Ag2+Ag3= Ag then
Ag =KA1Lg1Wg1+Ag2+KA2Lg2Wg2+KA3Lg3Wg3+…
Section 5) The Potential Utility of
Universal Formulas, Using The
General Area equation as An Example
There are a large number of formulas in mathematics and physics that can be generalized, into universal equations, but this does not necessarily imply that all of the resulting equations will have practical or theoretical utility. However, usually the generalized equation will provide at the very least a better understanding of underlying concepts. For example, with the general area formula (Ag=KALgWg) it is apparent that area is: length multiplied by width, multiplied by a constant (or coefficient) that relate to the geometric structure of the surface.
Usually, when a general formula is derived its practical or theoretical value may not be immediately apparent, and the idea is to attempt some creative thinking, and perhaps some experimentation to determine the utility of the equation. To illustrate some of these ideas I will return to the general area equation.
The potential utility of the Ag=KALgWg formula becomes apparent, when it is applied to complex geometric forms that CANNOT be divided into conventional geometric figures. Examples are the SURFACE AREA OF: mountainous terrain, crystals, catalysts used in chemistry, living cells, bacteria, viruses, molecules, atoms, as well as any surface that has peaks, valleys or holes. In general there is either a SPECIFIC value, or an AVERAGE value for KA for all of the above.
However, with
odd shaped objects, including all of the above, there is a
challenge to devise
a method of measuring the area,
and the
values for Lg and Wg, which are
needed to calculate
a SPECIFIC or AVERAGE value of KA,
in relation to a specific set of entities. This will
usually require more than
pencil and paper calculations, such as microscopic,
photographic, or
experimental techniques. With certain types of odd
shaped objects, it may be
feasible to calculate or estimate the area, length, and width
of the
structures, with digital photography, and the computer, by
counting pixels. However,
in some cases, there might be published data that can be used
to calculate or
estimate the value of KA
for a
specific entity.
The general area equation, Ag=KALgWg can be
used to calculate
the degree of roughness of a surface, if you have a method of
measuring Ag,
Lg
and Wg for
a square or
rectangular area. When the surface area of a square or
rectangle is perfectly
smooth KA=1.
When this
is not the case, KA
> 1.
Generally, the greater the value of KA
the rougher the surface will be. To use the general area
equation to calculate
the roughness of the surface, it is best to algebraically
rearrange as follows:
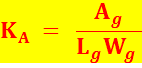
The technique
discussed in the above paragraph, can be carried out with a
circle, instead of
a square or rectangle. In such a case, 
A 
if
the surface is perfectly flat, without any bumps, holes or
peaks. A 
if
the surface is not perfectly flat.
It is
important to note that the concept of roughness and
smoothness are relative
concepts. For example, a flat piece of glass may look
perfectly smooth, but at
a molecular level it will be rough, and at an atomic level it
will be rougher.
This means that if you calculated the roughness of the glass
(as it appears to
the naked eye,) you would find that A
=1. However, if you had appropriate
equipment or the required
data to perform the calculations at the molecular or atomic
level the
value of KA would be greater than one.
A>1)
Section 6) Creating One General Equation From One or More Other General Equations
Section 6) Creating One General Equation
From One or More Other General Equations
It is often possible to create one general formula from one or more generalized equations, which can result in insight as well as new sets of equations. This can sometimes be achieved with algebraic manipulation and/or substitution of terms from one equation to another. Even an arithmetic operation, such as multiplication can sometimes result in a new equation as shown in the following paragraph.
A General
Volume Equation From The General Area Equation Ag=KALgWg:
A simple way of creating a general volume formula is to
multiply the general
area formula by height, represented by Hg
That is height multiplied
by area equals volume, with the following calculations: Hg(Ag=KALgWg) = HgAg = HgKALgWg.
HgAg = volume with this expression.
I am representing HgAg
with Vg.
With the resulting formula, the
constant KA, refers
to volume, so I
am representing it by KV.
(*To clarify this idea see the
note below.) Thus, the
general volume equation is Vg=KvHgLgWg
If you want to calculate the volume of a cube, a closet,
or a corrugated box, with
this equation: KV = 1,
Hg = height,
Lg = length,
and Wg = width. If you want to
calculate the volume of a
sphere, KV =
,
and Hg = r,
Lg = r,
Wg = r. If you want
to calculate the area of
a cylinder KV =
, Hg = height,
Lg = r,
and Wg = r
*Note, as PREVIOUSLY STATED: it is important to keep in mind that the value of the K terms are determined by the specific nature of the calculations, with The Theorem of General and Universal Equations, and with any other technique used in this e-book to derive general equations. That is by definition K represents the multiplier (a coefficient) that will yield the correct calculated results. If you derive any value for a K term that does NOT produce the correct calculated results, you have an INCORRECT value for K, which is true by definition.
Section 7) A General Equation for Distance
Section 7) A General Equation for Distance
The general distance equation, (DL = KD Dn) is a very simple formula, that I devised to represent the distance between two points, as measured with a straight line segment. DL represents the linear distance between two points. Dn represents the nonlinear distance between the two points, which can involve curved or zigzagged line segments. This can be restated in words, as follows: The linear distance (DL) equal the nonlinear distance (Dn) multiplied by a coefficient (KD). When Dn is multiply by the coefficient KD it equals the linear distance Dn Some examples will clarify this concept.
Let us assume the linear distance between TOWN‑A and TOWN‑B is 100 miles, but the travel distance between the two towns is 200 miles, because of the structure of the roadways. The value of KD can be calculated as follows: 100 = (200 )(KD) This simplifies to (100/200) = KD That is KD = 0.5 with this example. The value of KD (0.5) relates to the efficiency of the roads, in relation to the traveling distance between TOWNS A and B. This can be converted to a percentage which is 50%. Improving the roadways between the two towns, would increase the value of KD. If the roadways were perfectly redesigned to maximize the value of KD the roadways with represent a linear distance between the towns, and the KD would be equal to 1. However, with the general distance equation, KD can never be greater than one, assuming the calculations are based on real-world mathematics.
The general distance equation, (DL = KD Dn) can be further illustrated with a right triangle. This will become clear if you examine the right triangle presented below:
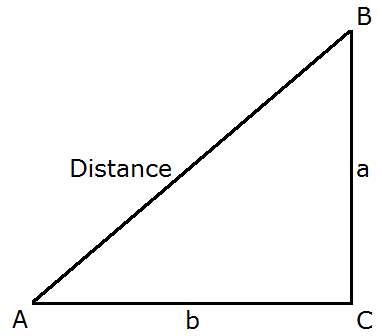
With the right triangle presented above, the linear distance is equal to the hypotenuse of the triangle, which can be represented as line segment AB. In addition, a+b is equal to the nonlinear distance between points A and B. However, the most important idea here is AB= KD(a+b) which is true but definition. Keep in mind that AB represents the linear distance in this case, and the equation can be rewritten as Distance = KD(a+b), or The Hypotenuse = KD(a+b). With a little algebraic manipulation it is obvious that the value of KD is equal to AB/(a+b). This relationship can also be represented as KD = Distance/(a+b).
If you examine the triangle, the mathematical relationships presented above, it becomes obvious that if angle A increases, the value of KD also increases. More precisely stated, as angle A approach 90 degrees, KD approaches 1. Thus, there is an obvious relationship between the concept of an angle, and KD.
The value of KD can easily be calculated, when the general distance formula involves a right triangle, with the Pythagorean theorem, (c2 =a2 +b2) as follows:
Distance = Hypotenuse = KD(a+b)=C
KD=C/(a+b)
Thus by substitution
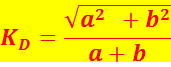
Section 8) Deriving the General Area and General Volume Equations with The General Distance Equation
Section 8) Deriving the General Area and
General Volume Equations with
The General Distance Equation
The general distance equation, (DL = KD Dn) discussed in the previous section, can be used to derive the general area equation by multiplication, as follows: The general area equation, Ag = KALgWg can be derived with the general distance equation, (DL = KD Dn) if we assume that DL1 = KD1 Dn1 and DL2 = KD2 Dn2 represent distances that relate to a specific area. With this assumption we can multiply (DL1)(DL2) to obtain the area, as illustrated below in a step-by-step way.
DL1=Lg
DL2 = Wg
Ag =Area = (DL1)(DL2) = (KD1)(KD2)(Dn1)(Dn2)
Ag =(KD1)(KD2)(Dn1)(Dn2)
KA=(KD1)(KD2)
(DL1)(DL2) = LgWg
Thus, by substitution Ag = KALgWg
The general distance equation, (DL = KD Dn) can also be used to derive the general volume equation (Vg=KvHgLgWg) by multiplication, as follows: We start by assuming that DL1, DL2 and ,DL3 represent distances that relate to a specific volume. Each of the three distances can be expressed by one of the following equations: DL1 = KD1 Dn1, DL2 = KD2 Dn2 and DL3 = KD3 Dn3 With this assumption we can multiply (DL1)(DL2)(DL3) to get to obtain the volume, as illustrated below in a step-by-step way.
DL = KD Dn
DL3=Hg
DL1 = Lg
DL2 =Wg
Vg =Volume = (DL1)(DL2) (DL3)
Vg = (KD1)(KD2) (KD3)(Dn1)(Dn2)(Dn3)
KV=(KD1)(KD2)(KD3)
(DL1)(DL2)(DL3) = KvHgLgWg
Thus, by substitution Vg = KVHgLgWg
*Note, as previously stated: it is important to keep in mind that the value of the K terms are determined by the specific nature of the calculations, with The Theorem of General and Universal Equations, and with any other technique used in this e-book to derive general equations. That is by definition K represents the multiplier (a coefficient) that will yield the correct calculated results. If you derive any value for a K term that does not produce the correct calculated results, you have an INCORRECT value for K, which is true by definition.
Section 9) The General Dimension Equation
Section 9) The General Dimension Equation
There are three generally accepted spatial dimensions, which are height, length, and width, which can represent perpendicular line segments of a geometric form. The line segments are linear and they form perpendicular angles with each other. However, there are theoretical concepts that define a number of additional dimensions.
In regard to the following equation, we can think of a dimension as a factor, in terms of multiplication. For example area is equal to two factors multiplied together, which is length multiplied by width, multiplied by a coefficient. Volume involves three factors multiplied together (height, length and width), multiplied by a coefficient. With this idea, we can create, a general dimension equation (or multiple dimension formula) with the general distance equation, or simply by multiplying a set of factors together, with a coefficient represented by Kg This results in the following equation:
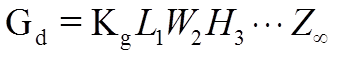
If we assume that all the factors have the same value, such as with the dimensions of a square, circle, cube, or sphere, we can represent the concept with the equation listed below.
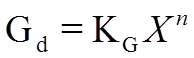
With the above equation, the exponent n, determines the meaning of Gd, when appropriate values for KG are utilized in the calculations, as follows:
When n = 1 Gd = distance,
When n = 2, Gd = the area of a square, or the surface area of cube, or sphere
When n = 3, Gd = the volume of a cube, or sphere
Both of the above equations represent an infinite set, which may contain undefined concepts that have practical or theoretical utility. For example, when the exponent is 0.25, 0.5, 4, 5,6 what would Gd represent?
Section 10) The General Energy Equation
Section 10) The General Energy Equation
The
formula for
kinetic energy is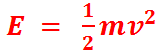 
.
This formula represents the energy
of a moving object, with a mass m,
and the
velocity v. This
equation can be generalized by
replacing the coefficient with KE.
Thus,
we can represent the general equation as follows:
Eg = KE mv2
The above equation represents many formulas that are used to calculate energy, including Einstein's equation E=mc2 With Einstein's equation KE = 1. We can even apply this equation to the energy of photons, by calculating the mass equivalent of a photon of a frequency of light. The mass equivalent to a photon can be calculated with Einstein's equation E=mc2 and E=hf (I am using f to represent the frequency of light, to prevent confusion with other symbols used in this e-book. h of course equals Planck's constant.) hf=mc2 Thus, the following is the mass equivalent of a photon m=(hf)/c2 It should be obvious from the formula that was derived, that the greater the frequency, the greater the mass equivalent, and the greater the energy of the photon.
Section 11) Deriving A General Temperature Equation, With The General Energy Formula
Section 11) Deriving A General Temperature Equation,
With The General Energy Formula
The temperature of an object relates to the kinetic energy of molecules and atoms that comprise the object. When a specific object is heated it gains energy, as its temperature rises. Thus, the General Energy formula can be applied to temperature of a solid, liquid or gas. In solids, and to some extent in liquids, v relates to frequency. Specifically, when molecules vibrate, even if they are moving back and forth, and not changing their position, they are still moving at a specific speed, which can be represented by v term in the general energy equation. In the case of a gas, the molecules are moving at an average speed that relates to temperature.
Thus, we can modify the General Energy formula to create a General Temperature Equation as follows Eg = KE mv2. T = KT mv2 with the above formula, T represents the Kelvin temperature, and m represents the molecular weight (molecular mass) and v represents the speed of the molecule and/or atom.
It is relatively easy to algebraically rearrange the General Energy equation, to derive a general formula to calculate the speed of moving particles, as follows:
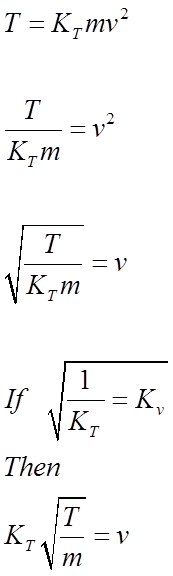
With the
equation derived abov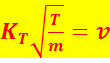e 
I
created a software-based
calculation device that calculates molecular speed, which
functions online over
the Internet. Left click on the following link to access
this calculation
device.
Physics Calculator for Molecular Speed
Section 12) The General Equation of Moving Particles
Section 12) The General Equation of Moving Particles
The concept described in the previous section, involving the representation of coefficients for a number of related equations with K, can also be applied to exponents. To demonstrate this concept, and its potential utility I will use the General Energy formula that was discussed in the previous sections. Eg = KE mv2 The General Energy equation represents calculations involving moving particles and objects, in terms of energy. However, if we modify this equation as follows, we will have an even more generalized equation that applies to, mass, momentum, and energy, as follows: PM = KM mvn. With this equation PM = energy, when n = 2 However, when n = 1, PM = momentum. When n = 0, PM = mass.
The interesting idea here is the equation PM = KM mvn defines an infinite set. It is apparent that there are three important concepts in the infinite set defined by this equation, which are mass, momentum, and energy. This raises the question are there other unknown or undefined concepts in this set, that may have practical or theoretical utility? See the following examples:
PM = KM mv0.25
PM = KM mv0.5
PM = KM mve
PM = KM mv3
PM = KM mv4
PM = KM mv5
PM = KM mv6
PM = KM mv-0.25
PM = KM mv-0.5
PM = KM mv-e
PM = KM mv-3
PM = KM mv-4
PM = KM mv-5
PM = KM mv-6
Below, there is a hyperlinked table of contents for this e-book. Left click on any of the blue words to go to the section of the e-book you want to read.
Section 3) The Theorem of General and Universal Equations
Section 4) Modifying a General Equation So It Will Apply To a Larger Number of Cases
Section 6) Creating One General Equation From One or More Other General Equations
Section 7) A General Equation for Distance
Section 8) Deriving the General Area and General Volume Equations with The General Distance Equation
Section 9) The General Dimension Equation
Section 10) The General Energy Equation
Section 11) Deriving A General Temperature Equation, With The General Energy Formula
Section 12) The General Equation of Moving Particles